Lagebeziehung von Geraden und Ebenen im $\mathbb{R}^3$

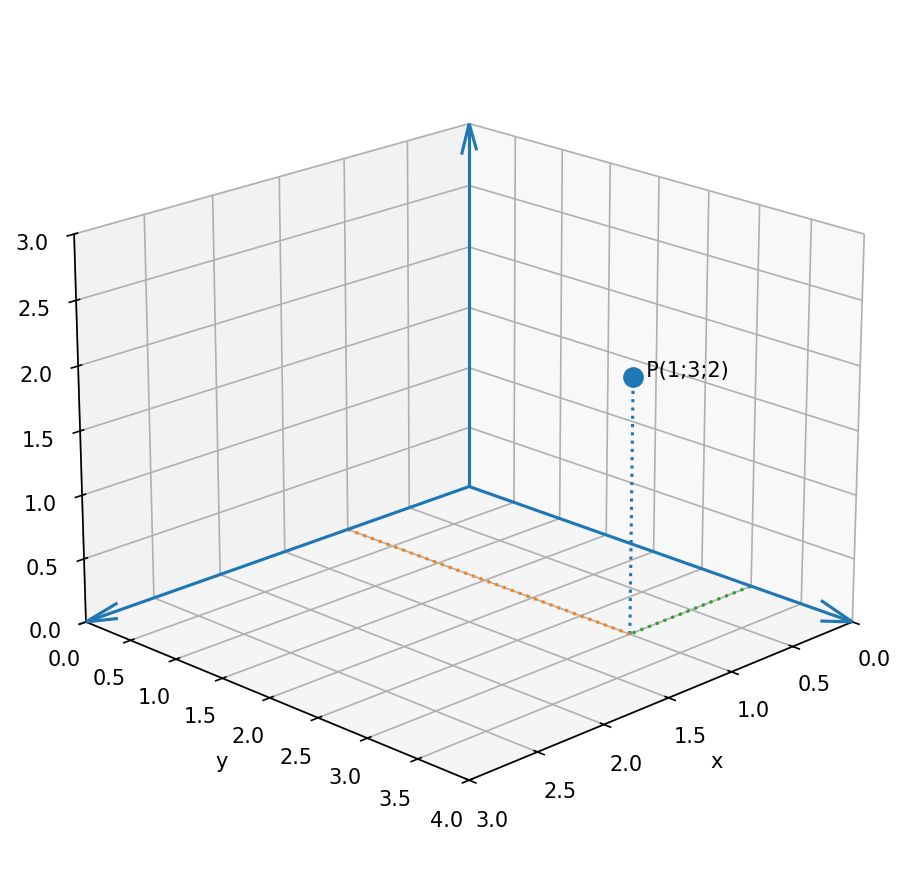
Ein Punkt im dreidimensionalen Raum wird durch drei Koordinaten beschrieben: $x$, $y$ und $z$. Diese drei Werte legen die genaue Position des Punktes im Raum fest.

Man notiert einen Punkt in der Form $P(x;y;z)$.

Skizze: Punkt $P(1;3;2)$ im Koordinatensystem

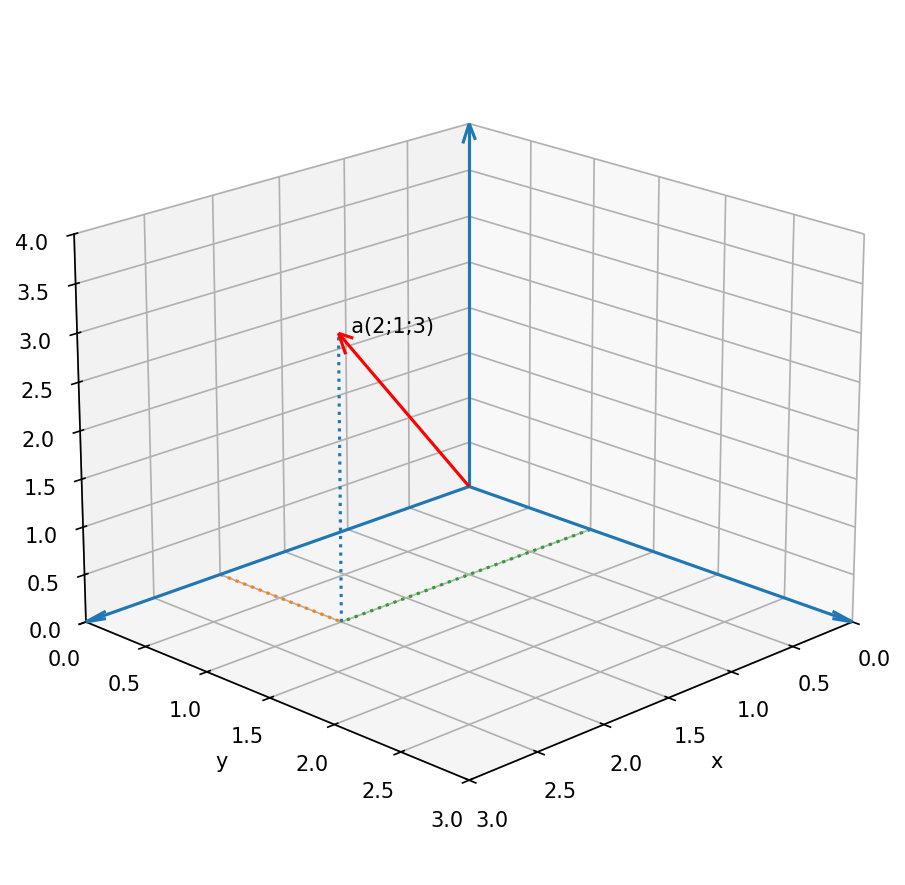
Ein Vektor beschreibt eine Verschiebung oder eine Richtung im Raum, zum Beispiel $\vec a(2;1;3)$.

Grafisch stellt man einen Vektor als Pfeil dar. Er besitzt immer eine Richtung und eine Länge.

Spitze – Fuß

Ein Vektor kann durch einen Startpunkt (Fuß) und einen Endpunkt (Spitze) beschrieben werden.

Beispiel:
Startpunkt $(0;0;0)$
Endpunkt $(1;1;3)$

Die Komponenten des Vektors erhält man, indem man Endpunkt minus Startpunkt rechnet:

$\begin{pmatrix} 1-0\\ 1-0\\ 3-0 \end{pmatrix} = \begin{pmatrix} 1\\ 1\\ 3 \end{pmatrix}$

Der Pfeil verläuft im Koordinatensystem also vom Startpunkt zum Endpunkt.

Beginnt ein Vektor im Ursprung $(0;0;0)$, so nennt man ihn Ortsvektor.

Alle Pfeile mit gleicher Länge und gleicher Richtung stellen denselben geometrischen Vektor dar – unabhängig davon, wo sie anfangen.

Vektor von $A(1;2;1)$ nach $B(4;5;3)$
Vektor von $C(0;1;2)$ nach $D(3;4;4)$

Beide Verschiebungen sind gleich lang und gleich gerichtet. Deshalb haben sie dieselben Komponenten:

$\overrightarrow{AB} = \begin{pmatrix} 3 \\ 3 \\ 2 \end{pmatrix}$

$\overrightarrow{CD} = \begin{pmatrix} 3 \\ 3 \\ 2 \end{pmatrix}$

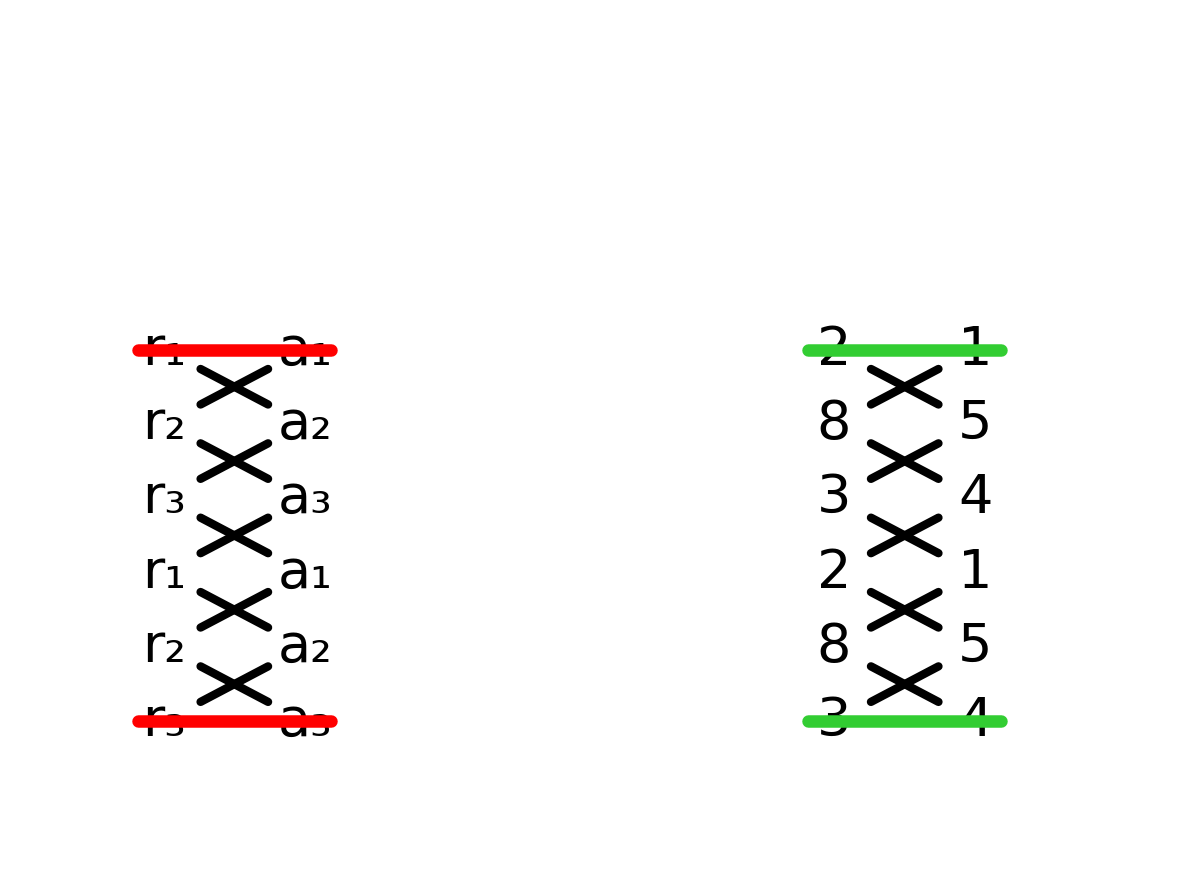
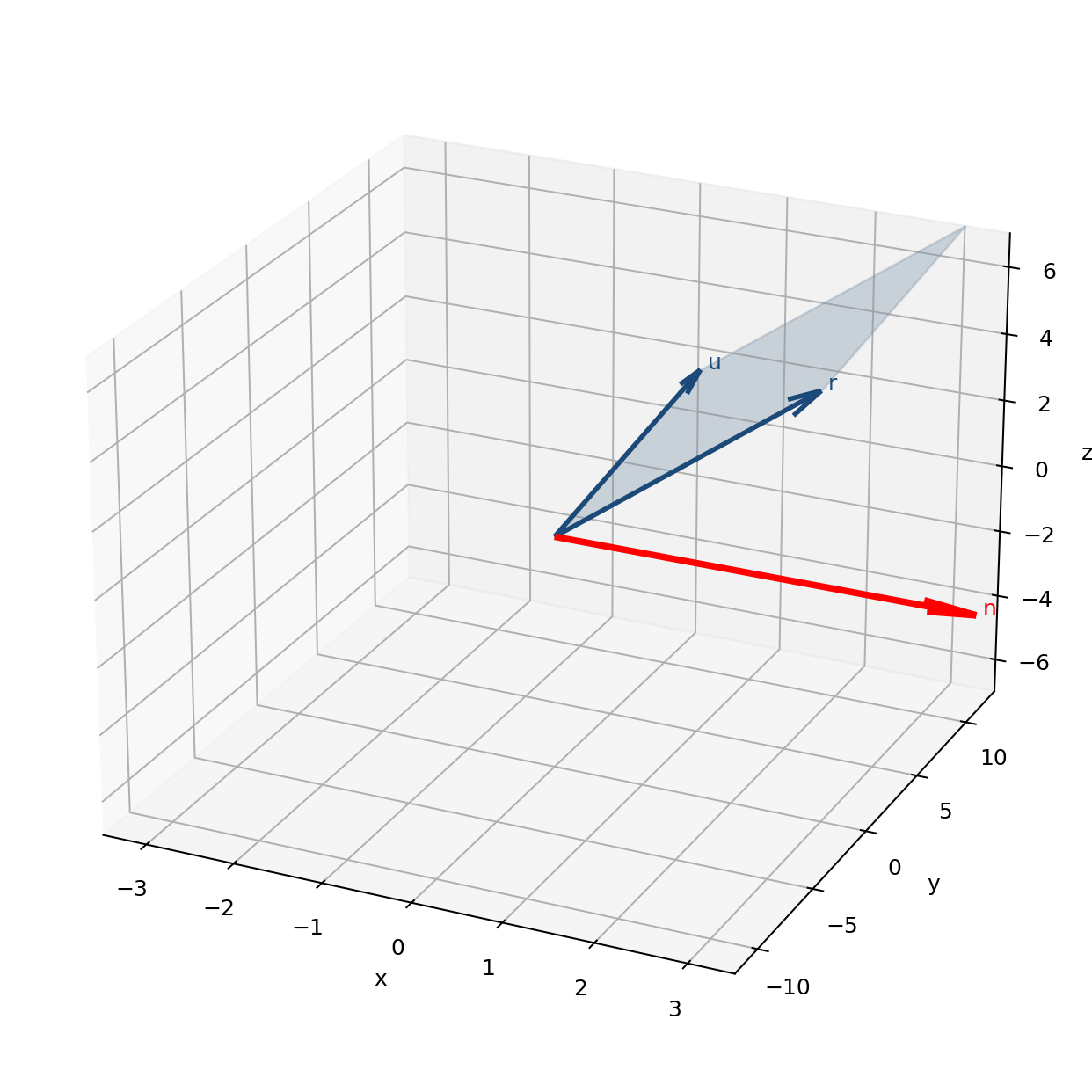
Kreuzprodukt der Richtungsvektoren

Eine Ebene wird durch zwei Richtungsvektoren aufgespannt. Ein Normalenvektor steht senkrecht auf dieser Ebene.

Den Normalenvektor kann man mithilfe des Kreuzprodukts der beiden Richtungsvektoren berechnen.

z. B.

$\vec r = \begin{pmatrix} 2 \\ 8 \\ 3 \end{pmatrix} \qquad \vec u = \begin{pmatrix} 1 \\ 5 \\ 4 \end{pmatrix}$

$\vec r \times \vec u$

Allgemein gilt:

$\begin{pmatrix} r_1 \\ r_2 \\ r_3 \end{pmatrix} \times \begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix}$

Berechnung der drei Komponenten:

$n_1 = r_2 \cdot u_3 - r_3 \cdot u_2 = 8 \cdot 4 - 3 \cdot 5 = 32 - 15 = 17$

$n_2 = r_3 \cdot u_1 - r_1 \cdot u_3 = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = -5$

$n_3 = r_1 \cdot u_2 - r_2 \cdot u_1 = 2 \cdot 5 - 8 \cdot 1 = 10 - 8 = 2$

Damit ergibt sich der Normalenvektor:

$n = \begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} = \begin{pmatrix} 17 \\ -5 \\ 2 \end{pmatrix}$

Das Kreuzprodukt und Parallelität

Das Kreuzprodukt zweier Vektoren liefert wichtige Informationen über deren Lage zueinander:

• Wenn $\vec{u} \times \vec{v} = \vec{0}$ (Nullvektor):
  Die beiden Vektoren $\vec{u}$ und $\vec{v}$ sind parallel zueinander (oder einer der beiden ist der Nullvektor). In diesem Fall spannen sie keine Ebene auf.
• Wenn $\vec{u} \times \vec{v} \neq \vec{0}$:
  Die beiden Vektoren sind nicht parallel. Sie spannen eine Ebene auf, und das Kreuzprodukt ergibt einen Normalenvektor, der senkrecht auf dieser Ebene steht.

Beispiel für parallele Vektoren:

$\vec{a} = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix} \qquad \vec{b} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$

Hier ist $\vec{a} = 2 \cdot \vec{b}$, also sind die Vektoren parallel.

$\vec{a} \times \vec{b} = \begin{pmatrix} 4 \cdot 3 - 6 \cdot 2 \\ 6 \cdot 1 - 2 \cdot 3 \\ 2 \cdot 2 - 4 \cdot 1 \end{pmatrix} = \begin{pmatrix} 12 - 12 \\ 6 - 6 \\ 4 - 4 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$

Das Kreuzprodukt ist der Nullvektor → die Vektoren sind parallel.

1. Skalar

Ein Skalar ist einfach eine reelle Zahl – kein Richtungspfeil, nur ein Wert.

$3,\; -2,\; \tfrac{1}{2},\; \pi$

2. Skalare Multiplikation

Ein Vektor wird mit einem Skalar multipliziert, das Ergebnis ist wieder ein Vektor.

$\lambda \cdot \vec{v} = \vec{u} \,\cdot\, 2 = 2 \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 6 \end{pmatrix}$

Bei positivem Skalar ändert sich nur die Länge, die Richtung bleibt.

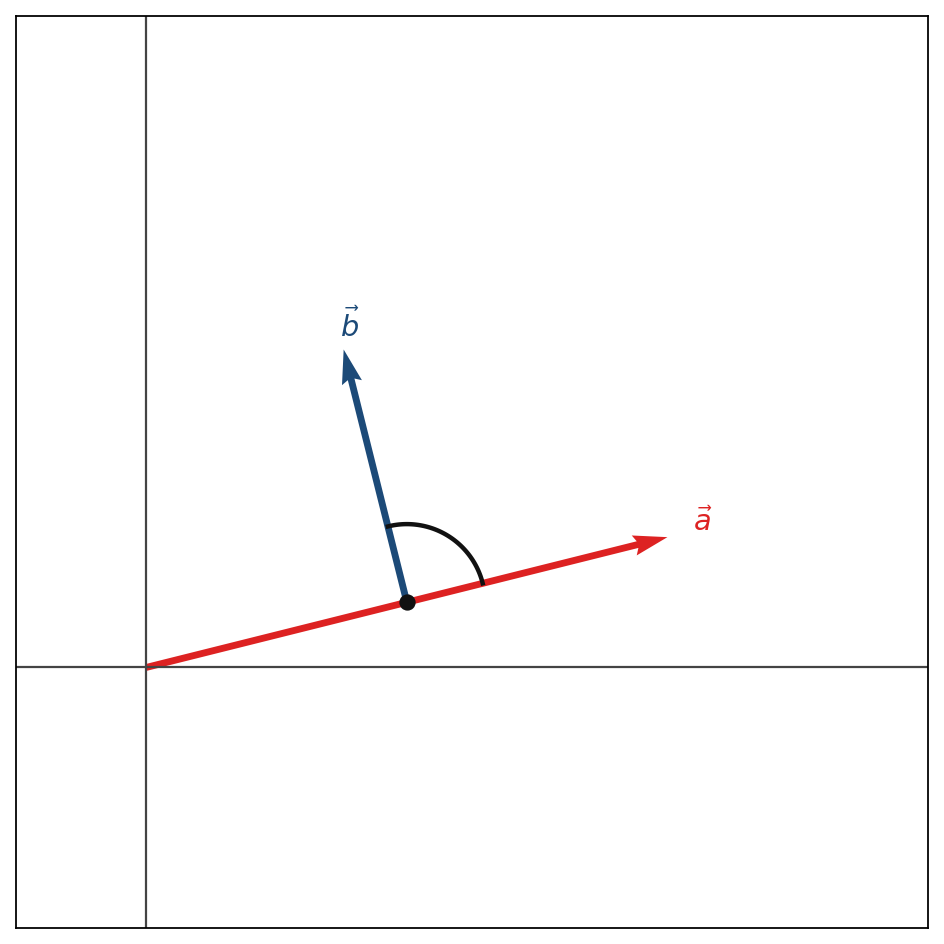
3. Skalarprodukt (Punktprodukt)

Verknüpft zwei Vektoren, Ergebnis ist ein Skalar (Zahl).

$\vec{a} \cdot \vec{b}$

Rechenform:

$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3$

Geometrisch:

$\vec{a} \cdot \vec{b} = \lVert \vec{a} \rVert \cdot \lVert \vec{b} \rVert \cdot \cos(\varphi)$

Orthogonalität (rechtwinklig): Zwei Vektoren stehen senkrecht zueinander, wenn ihr Skalarprodukt 0 ist.

$\vec{a} \perp \vec{b} \;\Longleftrightarrow\; \vec{a} \cdot \vec{b} = 0$

• Orthogonalität prüfen (rechtwinklig): $\vec{a} \cdot \vec{b} = 0$